From The Riddler comes “The perplexing puzzle of the prideful partygoers.” Let’s see if we can tackle this alliterative enigma.
The Problem
It’s Friday and that means it’s party time! A group of N people are in attendance at your shindig, some of whom are friends with each other. (Let’s assume friendship is symmetric — if person A is friends with person B, then B is friends with A.) Suppose that everyone has at least one friend at the party, and that a person is “proud” if her number of friends is strictly larger than the average number of friends that her own friends have. (A competitive lot, your guests.)
Importantly, more than one person can be proud. How large can the share of proud people at the party be?
Solution
Incorrect Solution
I’m embarrassed to say that I spent far too long on this problem going down the wrong solution path. However I believe you shouldn’t only post your successes, and the journey itself was instructive, so I’m still going to write about it.
Here we have a not-so-well disguised graph theory problem. The “party” is a graph, the “people” are nodes/vertices, and the “friendships” are edges. In jargon, we are being asked: “What is the largest possible proportion of nodes in a graph that have more edges than the average number of edges their neighbors have.”
Note that there is nothing stipulating that the graph is connected (i.e. we can have disjoint friend-groups) but we cannot have isolated nodes (since everyone has at least one friend). However, since we are being asked about the general strategy of constructing a graph that contains the highest proportion of proud partygoers, we can safely ignore instances where the graph may be unconnected (contains disjoint friend-groups), as that situation is simply a collection of smaller subproblems of our original problem.
As with most riddles, I started by considering the simplest case. In the depressing single node case, we don’t have party.
For 2 nodes, we do have a party, albeit a tame one. Perfect for gin, backgammon, chess, or digging into each other’s personal lives. In order for the graph to be connected, both partygoers must be friends with each other, and therefore each person has 1 edge, and their friends average 1 edge. Thus, no-one is proud.
A 3 person party is more fun than the 2 person party, but not as conducive to games. Perhaps cribbage? Monopoly? In fact, finding games that are fun to play with 3 people is such a challenge that I once spent an entire week with my cousins Mike and Jack trying to invent a catalogue of such games to fill the apparent gap. We did not do very well. Anyways, here we let Mike be friends with Jack and Drew, who are not friends with each other. Mike is proud, whereas Jack and Drew are not. Our proportion of proud people is \(\frac{1}{3}\).
With 4 people at our party, we’re cooking with gas! We’ve unlocked all the great classics like hearts, Catan, or bridge, and most board games with a flexible player number will feel “just right” with 4. Adding Dan to our party, we can let Mike be friends with Dan and Jack, and Dan be friends with Mike and Drew. Dan has 2 friends while his friends average 1.5 friends (Mike: 2 and Drew: 1). Mike is the same, so Mike and Dan are both proud and our proportion is \(\frac{2}{4}\)
From here, I thought I had figured out the solution. For the n person case, we let \(\frac{n}{2}\) partygoers be friends with each other, and then assign each of them 1 friend “outside” the inner circle. Thus, the inner \(\frac{n}{2}\) partygoers are proud and outer \(\frac{n}{2}\) partygoers are not. When we have an odd number of partygoers, we let the inner circle consist of \(\frac{n-1}{2}\) people. By constructing our graph in this way, the proportion of proud party members becomes 50%.
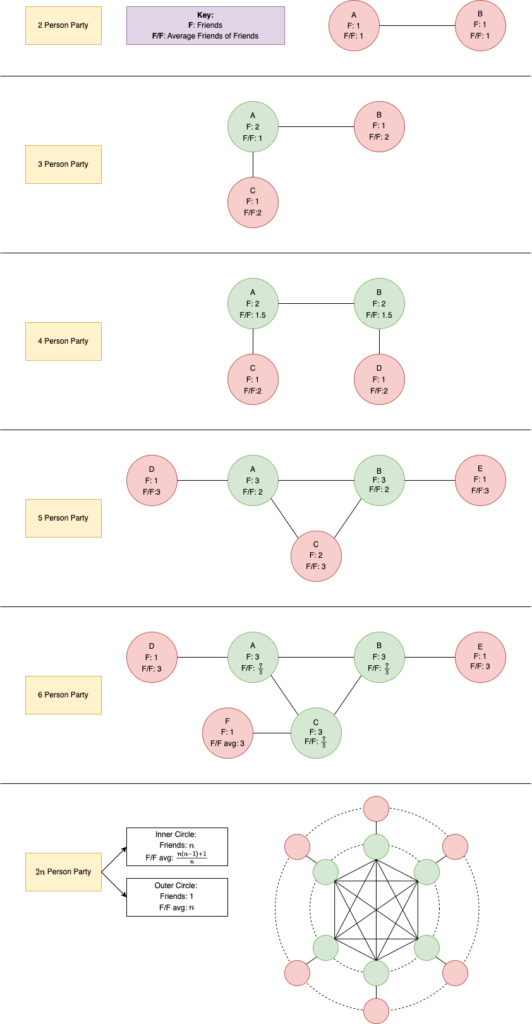
$$
\textbf{For a party with } 2n \textbf{ people} \\
\textbf{—————————————————————————————–} \\
\begin{align} \\
\text{Proud people} & = n \\ \\
\text{Proud people friends} & = n \\ \\
\text{Proud people average friends of friends} & = \frac{(n)(n-1) + 1}{n} \\ \\
\text{Non-proud people} & = n \\ \\
\text{Non-proud people friends} & = 1 \\ \\
\text{Non-proud people average friends of friends} & = n \\ \\
\end{align} \\
\textbf{—————————————————————————————–} \\
$$
We compute the inner circle’s average friends of friends by noticing that they have \(n-1\) inner circle friends with \(n\) friends each, and 1 other friend that has only 1 friend. To compute the average we take \((n-1)(n) + 1\) and divide it by \((n-1)+1\).
We can validate that the n inner circle partygoers are proud by using the fact that \(\frac{1}{n} < 1\).
$$
\textbf{Proof that } \frac{(n)(n-1) + 1}{n} < n \\ \\
\textbf{—————————————————————————————–} \\
\begin{align} \\
\frac{(n)(n-1) + 1}{n} &= n-1 + \frac{1}{n} \\ \\
&< n-1 + 1 \\ \\
&< n \\ \\
\end{align} \\
\textbf{—————————————————————————————–} \\
$$
The correct solution
Hopefully, unlike me, you didn’t spend 30 minutes drawing out all these diagrams to realize not only was your answer was wrong, but also the correct answer is much simpler (double whammy)! While squinting at the inner circle graph on my last diagram, I realized that if I ignored the outer circle and just removed 1 edge between two partygoers, then everyone else in the inner circle becomes proud. For lack of a better option, let’s call the two people who lose an edge “losers”, and everyone else “popular”.
Using this methodology, we construct a complete graph (everyone is friends with everyone), and then remove 1 edge. The 2 losers now have 1 fewer friend than everyone else, and everyone else is proud.
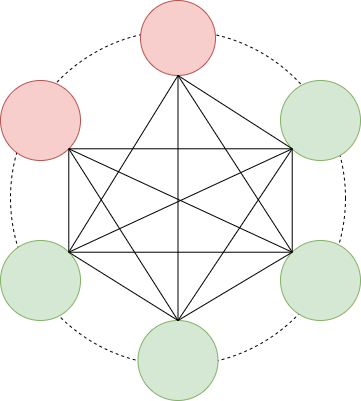
$$
\textbf{For a party with } n \textbf{ people} \\
\textbf{—————————————————————————————–} \\
\begin{align} \\
\text{Proud people} & = n-2 \\ \\
\text{Proud people friends} & = n-1 \\ \\
\text{Proud people average friends of friends} & = \frac{(n-3)(n-1) + 2(n-2)}{n-1} \\ \\
\text{Non-proud people} & = 2 \\ \\
\text{Non-proud people friends} & = n-2 \\ \\
\text{Non-proud people average friends of friends} & = (n-1) \\
\end{align} \\
\textbf{—————————————————————————————–} \\
$$
We compute the popular partygoer’s average friends of friends by noticing that they have \(n-3\) popular friends with \(n-1\) friends each, and 2 loser friends with \(n-2\) friends each. To compute the average we take \((n-3)(n-1) + 2(n-2)\) and divide it by \((n-3)+2\).
We can validate that with this set up, the \(n-2\) popular partygoers are proud by using the fact that \(\frac{n-2}{n-1} < \frac{n-2}{n-2}\).
$$
\textbf{Proof that } \frac{(n-3)(n-1) + 2(n-2)}{n-1} < n-1 \\
\textbf{—————————————————————————————–} \\
\begin{align} \\
\frac{(n-3)(n-1) + 2(n-2)}{n-1} &= n-3 + \frac{2(n-2)}{n-1} \\ \\
&< n-3 + \frac{2(n-2)}{n-2} \\ \\
&< n-3+2 \\ \\
&< n-1
\end{align} \\
\textbf{—————————————————————————————–} \\
$$
Therefore for a party with \(n\) people, we can construct a social graph where \(n-2\) of them are proud. Under this construction, if there are 60 people at our party, 58 of them are proud. As n gets higher and higher, the proportion of proud party members approaches 100%.
$$
\lim_{n\to\infty} \frac{n-2}{n} = 1
$$
In a world where everyone is proud, is anyone proud?
