CHAMP: Can we count to 100? – Drew Mathieson's Blog

Every couple of weeks, a member of the Branson Math department, Dave, sends out a “CHAMP” to our student body. CHAMP usually stands for “Challenge: Here’s a Math Puzzle,” but sometimes Dave adjusts the acronym to something more apt to the problem itself. Most recently, it was Challenge: Help Alchemist Make Potion, and the problem was a clever reframing of the google horse-racing interview question.

These CHAMPs are often interesting and approachable, making them great candidates for blog posts. In particular, I’m interested in exploring the CHAMPs that lend themselves nicely to programatic solutions, as they tend to be mild in scope which is perfect for someone trying to learn python! With that being said, here’s the problem.

Context

Consider the ascending sequence of digits $123456789$ and the operations $+$ and $-$.
If you combine substrings of these 9 digits in order, along with some combination of $+$ and $-$ signs, you create an expression equal to a number. For example:

$$12+34-5+678-9=710$$

You can do the same thing with the descending sequence of digits $987654321$. For example:

$$-9+8-76-5+4+3+21=-54$$

Problem statement

1. Combine the sequence of digits $123456789$ and the operations $+$ and $-$ to create an expression that equals $100$.

2. Combine the sequence of digits $987654321$ and the operations $+$ and $-$ to create an expression that equals $100$.

Give it a shot!

Finding a general approach

We begin by finding a solution to #1 using guess and check (never a bad place to start). By noticing that $123$ is to $100$, we can hone in on a solution by starting with $123$ and then working on reducing it to $100$ using the remaining 6 numbers. After some trial and error we arrive at a valid solution.

$$123-4-5-6-7+8-9=100$$

This approach demonstrates why this problem is a good candidate for being solved recursively. Namely, after we start with $123$, we have reduced the original problem to a simpler version of itself, where we want to use the digits $456789$ to obtain a target value of $-23$.

To find a general solution to problems of this form, we consider a function $solve(input, target)$ which takes as input a list of digits (eg: $123456789$) and a target value (eg: $100$). We can then recursively call the $solve()$ function within itself on smaller and smaller sub-problems of our original inputs.

In our above example, we turned $solve(123456789, 100)$ into the simpler $solve(456789, -23)$. We did this by removing the substring $123$ from our input and also subtracting $123$ from our target.

Our simplest case (aka our base case) will be when our input has length 0, and will be successful if our target is also 0 (and fails if our target is non-zero).

Simple example

As an example, let’s try to solve the problem for an input of $1234$ and a target of $5$. We can quickly see that $12-3-4=5$ is a solution.

To find all possible solutions, we will want loop through each of the possible starting substrings of $1234$, as well as consider making each substring positive or negative.

The first substring is $1$, and we have to consider both $+1$ or $-1$. If we choose $+1$, our new target is $4$. If we choose $-1$ our new target is $6$ (we must add $6$ to $-1$ in order to get to our original target value of $5$). Thus, we are left with the following two sub-problems: $solve(234, 4)$ and $solve(234, 6)$.

Our second substring is $12$ and we consider $+12$ or $-12$. If we choose $+12$, our new target is $-7$. If we choose $-12$ our new target is $17$. Thus, we make the following two calls: $solve(34, -7)$ and $solve(34, 17)$.

This process would continue for the substrings $123$ and $1234$…

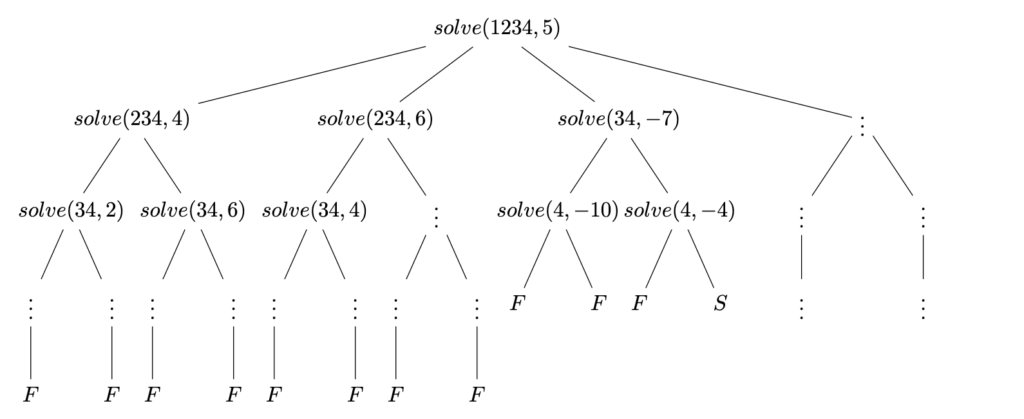
Recursion tree

A recursion tree for this example is illustrated below, where a branch terminating in an F indicates failure to find a solution (the input is empty and the target is non-zero), and a branch terminating in an S indicates a valid solution path was found (the input is empty and $target=0$).

I’ve only filled in part of the tree as the complete tree would have been tedious to draw. Notice we can find our $12-3-4$ solution by going down the branch that starts with $12$!

Giving the solve function a memory

One final tweak of our function is needed before we’re ready to tackle our two problems. As it’s currently described, our solve function can find/validate different solution paths, but it can’t actually remember what that solution path was.

We need to build our function a “memory” so that we can keep track of the choices made by our higher up $solve()$ calls. By appending the current choice of substring to a string of past choices, we can pass this argument (let’s call it “solution_path”) through the function and keep track of the potential solutions as we go. When we find a successful solution, we have a record of the full solution path, and append it to a list of other found solutions.

Coding our solve function

Now let’s write our solve function. As with many recursion problems, this seemingly complex problem can be solved with only a few lines of code! Also, I didn’t realize input was a key word for python, so I used the variable x instead.

def solve(x, target, solution_path, solutions):
  if len(x) == 0:
      if target == 0:
          solutions.append(solution_path)
  else:
      for i in range(0, len(x)):
        substring = x[:i+1]
        remaining_digits = x[i+1:]
        solve(remaining_digits, target + int(substring), solution_path + "-" + value, solutions) 
        solve(remaining_digits, target - int(substring), solution_path + "+" + value, solutions)

Displaying our solutions

x_1 = '123456789'
x_2 = '987654321'
target = 100
solutions_1 = []
solutions_2 = []

solve(x_1, target, "", solutions_1)
solve(x_2, target, "", solutions_2)

print("Solutions for " + x_1 + " = " + str(target))
for s in solutions_1: 
  print(s)
print("Solutions for " + x_2 + " = " + str(target))
for s in solutions_2: 
  print(s)

## Solutions for 123456789 = 100
## -1+2-3+4+5+6+78+9
## +1+2+3-4+5+6+78+9
## +1+2+34-5+67-8+9
## +1+23-4+5+6+78-9
## +1+23-4+56+7+8+9
## +12-3-4+5-6+7+89
## +12+3-4+5+67+8+9
## +12+3+4+5-6-7+89
## +123-4-5-6-7+8-9
## +123+4-5+67-89
## +123-45-67+89
## +123+45-67+8-9

## Solutions for 987654321 = 100
## -9-8+76-5+43+2+1
## -9+8+7+65-4+32+1
## -9+8+76+5-4+3+21
## +9-8+7+65-4+32-1
## +9-8+76-5+4+3+21
## +9-8+76+54-32+1
## +9+8+76+5-4+3+2+1
## +9+8+76+5+4-3+2-1
## +98-7-6-5-4+3+21
## +98-7-6+5+4+3+2+1
## +98-7+6-5+4+3+2-1
## +98-7+6+5-4+3-2+1
## +98-7+6+5+4-3-2-1
## +98+7-6-5+4+3-2+1
## +98+7-6+5-4-3+2+1
## +98+7-6+5-4+3-2-1
## +98+7+6-5-4-3+2-1
## +98-76+54+3+21

We see that there are 12 solutions for #1, including the only solution accross both questions to use only 4 substrings.

$$123-45-67+89=100$$

There are 18 solutions for #2, including an almost as cool 5 substring solution. $$98-76+54+3+21=100$$.

Extensions

Positive vs. negative starting substring

To me, the most striking thing when looking over our results is that only 4 of our 30 combined solutions start with a negative number. While I expected positive starting numbers to be more prevalent (we were aiming for a positive target value after all), only $\frac{4}{30}$ seems very low. I dug deeper to see if the pattern held for target values near 100 with our input of $123456789$.

for target in range(90, 110):
  solutions_1 = []
  neg = 0
  pos = 0
  solve(x_1, target, "", solutions_1)
  for s in solutions_1:
    if s[0] == "+": 
      pos+=1
    else: 
      neg+=1
  print(str(target) + ": " + str(pos) + " pos " + str(neg) + " neg.")

## 90: 14 pos 7 neg
## 91: 16 pos 6 neg
## 92: 13 pos 8 neg
## 93: 11 pos 12 neg
## 94: 11 pos 6 neg
## 95: 10 pos 7 nega
## 96: 11 pos 8 neg
## 97: 7 pos 14 neg
## 98: 9 pos 6 neg
## 99: 17 pos 8 neg
## 100: 11 pos 1 neg
## 101: 10 pos 8 neg
## 102: 8 pos 11 neg
## 103: 9 pos 5 neg
## 104: 11 pos 3 neg
## 105: 6 pos 12 neg
## 106: 7 pos 11 neg
## 107: 11 pos 6 neg
## 108: 15 pos 4 neg
## 109: 7 pos 5 neg

So while we did see more positive starting solutions than negative starting solutions in general, 100 is still quite an outlier with only 1 negative solution. Numbers very close to it, like 102, have more negative starting solutions than positive! Let me know if you have a good explanation for why that is…I’m stumped. Is 100 just an outlier? Or is there some property of the number that can help explain this pos/neg split?

I also generated this list for the input of $987654321$.

## 90: 16 pos 4 neg
## 91: 8 pos 6 neg
## 92: 15 pos 5 neg
## 93: 9 pos 8 neg
## 94: 19 pos 4 neg
## 95: 10 pos 5 neg
## 96: 16 pos 3 neg
## 97: 9 pos 7 neg
## 98: 12 pos 4 neg
## 99: 11 pos 11 neg
## 100: 15 pos 3 neg
## 101: 9 pos 6 neg
## 102: 19 pos 4 neg
## 103: 9 pos 3 neg
## 104: 13 pos 3 neg
## 105: 8 pos 5 neg
## 106: 11 pos 5 neg
## 107: 9 pos 6 neg
## 108: 13 pos 6 neg
## 109: 8 pos 4 neg

Note that 100 was less of an outlier here, but $987654321$ has more bias towards starting with positive numbers. Perhaps this is because starting with $-9$ or $-98$ puts you further from $100$ than starting with $-1$ or $-12$.

Target value vs number of unique solutions

The last thing I did was create some graphs plotting the number of unique solutions against various target values (not just $100$).

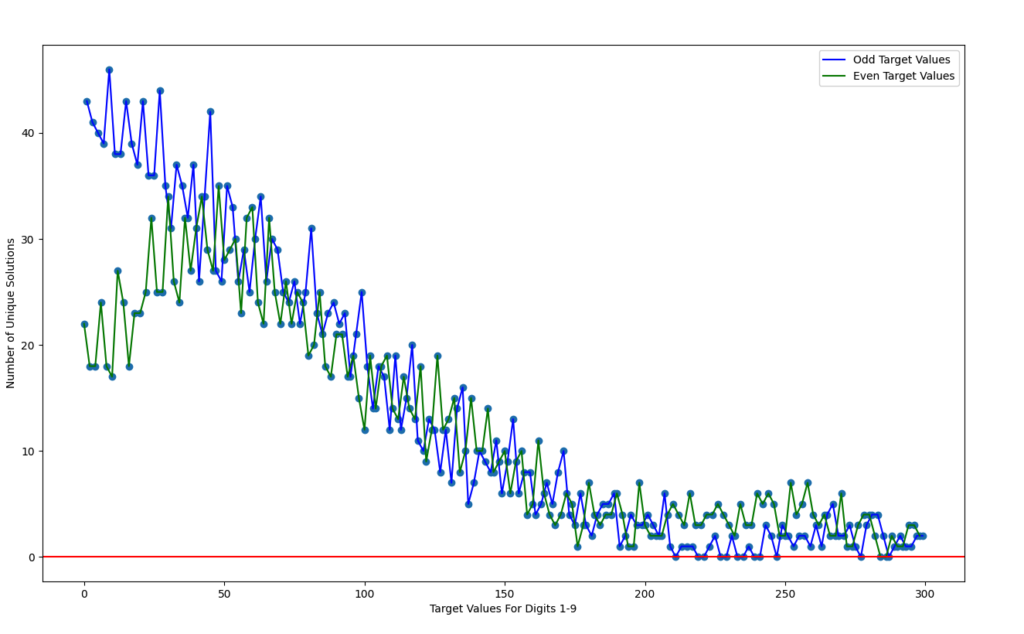
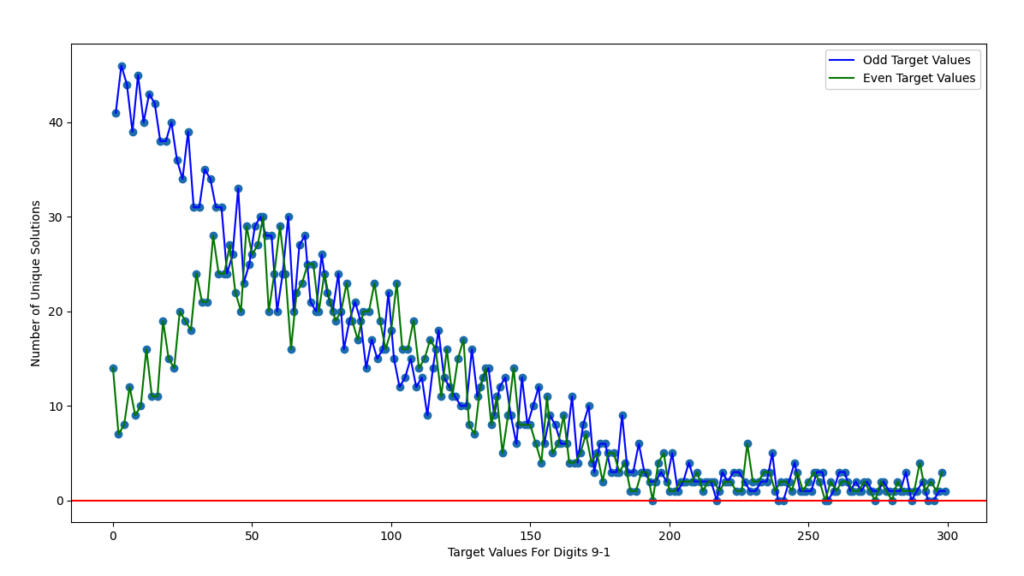
As expected, the further the target gets from 0, the fewer solutions we are able to find. Interestingly, for small target values, odd numbers have many more solutions than even numbers.

My hypothesis is that this occurs because for small target values, we can often find solutions using no 2 or more digit substrings. If we use all 9 1-digit numbers, our solution is the addition or subtraction of 5 odd numbers and 4 even numbers, which results in an odd number. Additionally, if we use only one 2 digit substring and seven 1 digit substrings, we will still end up with an odd number half the time (depending on if the 2 digit substring is even or odd). Thus, it is “easier” to obtain small odd numbers. Any solution that results in an even number cannot use only 1 digit substrings.

Some evidence to collaborate this hypothesis is that for a target value of $3$, there are $23$ unique solutions that involve only 1 digit substrings. Those 23 solutions alone can explain the difference between the number of solutions for $3$ vs $2$. As our numbers get larger, the number of solutions involving only 1 digit substrings diminishes (and becomes $0$ after $45$), so the odd/even split falls away.

Unsolvable target values

The first occurrence of an “unsolvable” target value is $211$ for $123456789$ and $194$ for $987654321$. I suspect these numbers are fairly random artifacts of our initial list of inputs (i.e. if we choose a different starting input, there is no reason to think $211$ will be a “hard” number to reach as compared to any other around it).

Future directions

I think the most interesting path to explore would be different starting substrings. I think a fascinating question to try to answer would be “Which starting substring” gives the most unique solutions for a target value of $100$.” How does that “best” substring change when our target value changes? As a specific example, for which targets would a substring like $123234345$ give more solutions than our original $123456789$.

Let me know if you gave this problem a try and what you learned!